|
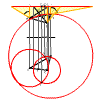
Fig. 13
|
Note: Dû aux limites des logiciels courants, le cône est spécifié
par un cercle ou une ellipse, et une hauteur. Le cône, théoriquement
infini, est donc, à priori, tronqué quelque part par un plan. Il en
résulte que la courbe d'intersection n'est pas toujours complète. Dans
l'exemple illustré, la courbe d'intersection des cônes B et C est complète,
celle des cônes A et C l'est presque alors que celle des cônes A et
B est très partielle. Pour l'obtenir au complet, il suffit d'augmenter
la hauteur des cônes suffisamment.
Construction géométrique
Pour faire la construction des courbes d'intersection, on construit
le plan et l'élévation des 3 points connus A, B et C. On construit en
élévation les génératrices des cônes sous l'angle vertical connu (a°
pour A, b° pour B et c° pour C). On coupe les 3 cônes par un plan horizontal
ce qui détermine les 3 rayons à cette hauteur que l'on reporte en plan
sous forme de 3 cercles de centre A, B et C. L'intersection des cercles
deux à deux (1 et 2) donnent des points sur l'intersection que l'on
reporte en élévation (1' et 2'). Un point particulier de l'intersection
dans le plan passant par les deux sommets (A et B) peut être calculé
en élévation (3') par l'intersection des génératrices contenues dans
ce plan et reporté en projection horizontale (3).
Tout nouveau plan de coupe horizontal définira de nouveuz cercles et
donnera de nouveaux points d'intersection. Chaque courbe d'intersection
peut ainsi être calculée en plan et en élévation.
|